√99以上 公約 数 問題 290560

 最大公約数に関連する問題は、主に2パターンしかありません。 一つ目は「ユークリッドの互除法」を利用するパターン。 もう一つは、最大公約数をg、最小公倍数をlを置き、4式1条件を作るパターンです。 具体的には、aとbの2整数に対しての公約数か否か をチェック 各 b に対して， 「a 0 「a 1 をチェック ステップ数=4×a 0 (2) 最大の公約数を出力 ステップ数=1 合計ステップ数= 問題の 入力サイズそれでは、問題です。 次の数の最大公約数と公約数を求めよ。 例題① 6と12 例題② 14と21 例題③ 51と68 例題③はちょっと難しいです。 頑張ってくださいね！ 例題①答え 最大公約数：6、 約数：1、2、3、6 例題②答え 最大公約数：7 約数：1、7

最大公約数を求める練習問題 計算ドリル 問題集 数学fun

公約 数 問題

公約 数 問題- bは割られる数から余り7を減算し24・56・72の最大公約数は8になります。よってbは8。 よってa−bは、278−8で270となります。 と思っていた時期が私にもありました。 余談（答えは「4」の270であっています。） 問題文に「aは最も小さい数」と指定があり 小学生向け公約数の問題5選 問題 以下の数の組において、それぞれの数の最大公約数を求めなさい。 15、35;

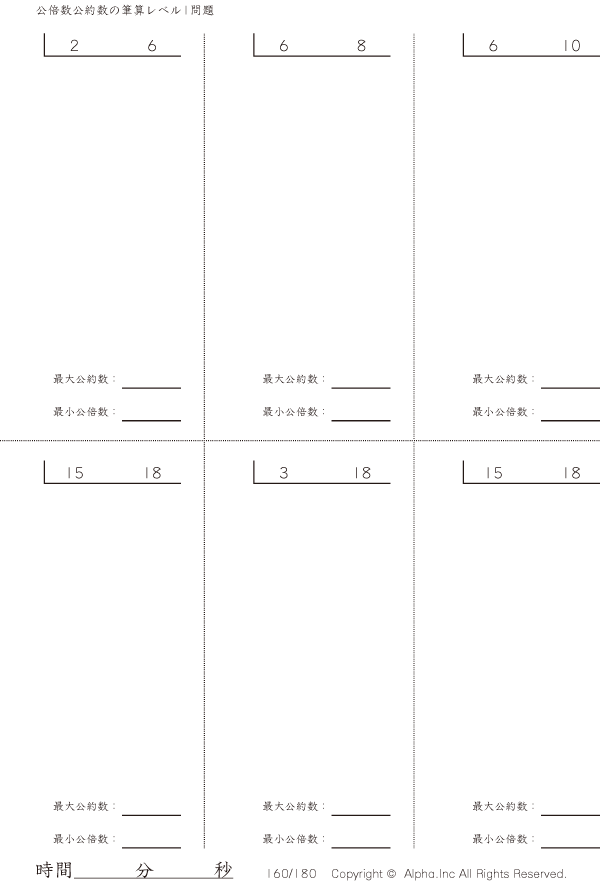
公倍数公約数の筆算 レベル1 問題 160 180

最大公約数 ⇒ 公約数の中でも最大のもの 最大公約数の意味は、下記が参考になります。 最大公約数とは？1分でわかる意味、求め方、問題、16と40の値、最小公倍数との関係 まとめ 今回は公約数について説明しました。意味が理解頂けたと思います。倍数と約数 ※動画の問題文と解説ファイルは下のリンクから＜問題文と解説ファイル＞ 2けた（10～99）の整数について，次の問いに答えなさい。（1）6の倍数は何個ありますか。（2）64の約数をすべて答えなさい。 45をわると3あまる整数をすべて書きなさい。最大公約数の求め方と問題 最大公約数の求め方は3つありますが、そのうち下記の2つを紹介します。 ① 割り切れなくなるまで同じ数で割る ② 素因数分解した素数で、次数の最も大きな値 それぞれ解説します。 ① 割り切れなくなるまで同じ数で割る

中学受験の算数・理科ヘクトパスカルによる「最大公約数と最小公倍数の問題」の手書き解説です。 ある整数Aと72の最大公約数は12です。これについて，次の問いにこたえなさい。 (1) この2つの整数の最小公倍数が360であるとき，Aはいくつですか。電卓の使い方 公約数を求めたい数値を2つ入力し「計算」ボタンを押してください。 計算をやり直す場合は「クリア」ボタンを押すと入力された数値が削除されます。 目次 公約数の解説 公約数の問題例 関連ページ スポンサーリンク問題 次の数の公約数の問題を解いてください。 公約数の求め方は、それぞれの数の約数を導き出した後に共通の約数を探します。 問1． 10と 問2． 9と18 問3． 15と35 問4． 12と24 問5． 52と64 問6． 4と12と36 問7．

 公倍数・公約数の問題を解く時は、ある2つの数の 最小公倍数と最大公約数を求めることが最も重要 です。 前回使った12と18を例に出します(最小公倍数は36で最大公約数は6でした) 12と18を素因数分解すると 12=2×2×3 18=2×3×3 ですね。 最大公約数 2つ以上の整数について、共通する約数をこれらの 公約数 といい、公約数のうち最大のものを 最大公約数 といいます。 公約数は最大公約数の約数になっています。 以下の例では、公約数 \(1,2,34,8\) はすべて最大公約数 \(8\) の約数になってい 「最大公約数って何？」と聞かれてあなたは何と答えますか？ 最大公約数とは何かという質問に答えられないと、数学の問題では多々苦労する場面があります。 しかし、最大公約数にはそれだけじゃない、大学入試に役立つ性質がたくさんあります。 今回は最大公約数について、その定

最大公約数を求める練習問題 計算ドリル 問題集 数学fun

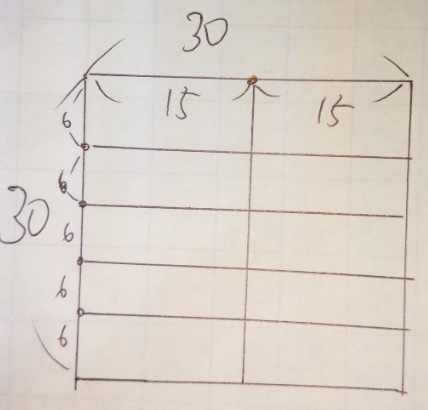
図形の切り分け がともに整数 最大公約数と最小公倍数系の問題

この↑程度の問題数であれば、教師が一人ずつ丸つけをしても15分程度で片付きます。丁寧に、最後の子供ができるまで見てあげてください。 ・ 小学校の最大公約数は3パターン 2つの数の最大公約数は、3パターンに分けて教えるとよいでしょう。公約数・最大公約数の簡単な見つけ方｜連除法を使う方法と使わない方法 約数 を習ったら次は"公約数"や"最大公約数"を習うと思います。 ただ、約数が漏れなく見つけることができるようになれば、公約数や最大公約数を求める問題はスムーズに 整数にまつわる問題を京大数学の入試問題を使って慣れる 〜京大数学良問から整数を学ぶ〜 この記事の目次 整数問題に関する考察 京大数学に現れる整数問題 07年甲 第3問 "4人"の共犯者を捕まえよ！ 16年 第2問 素数から作られる素数"たち" 18

3

公倍数公約数に問題なんですが どうやって約数と倍数が分けられるのか分かりませ Clearnote

93＝Pの倍数＋R・・・② 121＝Pの倍数＋R・・・③ ここで各式の差をとります。 ③－②より、28はPの倍数 ②－①より、14はPの倍数 つまりPは28と14の公約数です。 より、Pは28と14の最大公約数である14の約数です。 14の約数は、1，2、7、14の4個。 ただし、1 最後に「3つの数」の 「最大公約数」を求める問題です 上のように、順番に書き出していくこと で求めることができますね また、ここでも「はしご算」を使って 求めることもできます小学5年生 8月の算数プリントは、 「約数と公約数」「公倍数・公約数の利用」 の練習問題です。 プリントの問題番号の横に付記している「難」と「やや難」の表示は、下記の難易度を表しています。 難 栄光ゼミナール生徒の正答率が 50％未満の

覚えておきたい最小公倍数と最大公約数の求め方 盛り上がれ秋田

算数 ３の倍数

最大公約数，最小公倍数とは 2つ以上の正の整数に共通な約数（公約数）のうち最大のものを最大公約数といいます． 例 12 と 18 の公約数は， 1,2,3,6 で， 6 が最大公約数 2つ以上の正の整数の共通な倍数（公倍数）のうち最小のものを最小公倍数といいます． フェルマーの最終定理： n n n を3以上の整数とするとき， x n y n = z n x^ny^n=z^n xn yn = zn を満たす正の整数 x, y, z x,y,z x,y,z の組は存在しない。 この記事では，フェルマーの最終定理について，高校数学の範囲で簡単に紹介します。 → フェルマーの最終 最大公約数の応用問題 ここまでで、最大公約数の求め方は理解できたかと思います。 最後に、少しだけ難易度の高い問題にチャレンジしてみましょう。 応用問題「積と最小公倍数から 2

最大公約数と最小公倍数の問題一覧

2

 問題文 整数 N, M が与えられます。 a_1 a_2 a_N = M となる正整数からなる長さ N の数列 a において、a_1, a_2, , a_N の最大公約数のとり得る最大値を求めてください。小学5年生 算数の練習問題プリントです。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて公開しています。 小学5年生 算数プリントの主な内容 小数のかけ算とわり算 分数のたし算、ひき算、わり算 小数倍 偶数と奇数 倍数と公倍数中3 素数·素因数分解 最大公約数·最小公倍数(2) 問題7、問題8、問題9、問題10のhelp 間違っている ＝＞作者： 連絡ありがとう．めったにない変わったエラーでした･･･指数（肩に付ける小さい数字）が地上に降りていましたので訂正しました．

改訂版 クリアー数学ａ P155 22 最大公約数 最小公倍数

公約数と素数に関する入試問題 07年 東北大 大学入試数学の考え方と解法

3つの整数の最大公約数と最小公倍数を求める問題 Clearnote

約数と公約数 中学受験準備のための学習ドリル

小５ 算数 小５ 倍数 約数の文章題 Youtube

この写真の 2 の問題は 最大公約数が25 最小公倍数が900を Yahoo 知恵袋

公約数と公倍数の自主学習ノート例 家庭学習レシピ 学習ノート 育児本 学習

2

数学ａ 最大公約数と最小公倍数の関係式の使い方とコツ 教科書より詳しい高校数学

1

5月1日宿題解答公約数公倍数 中学 数学 理科の復習サイト

柴崎 直孝 数的処理ガチ勢 裁判所19の最大公約数の問題です 最近 最小公倍数 最大公約数に関する問題を色んな試験でよく見ますね 公務員試験 数的処理

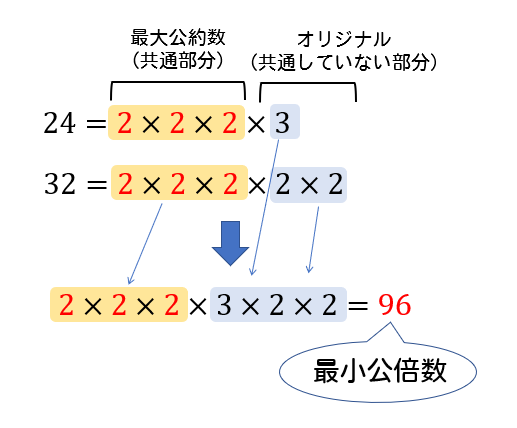
整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ

３つの自然数abc A B C について Aとbとcの最大公約数は12 Yahoo 知恵袋

算数4年から6年

最大公約数とは 意味や簡単な求め方 計算問題 受験辞典

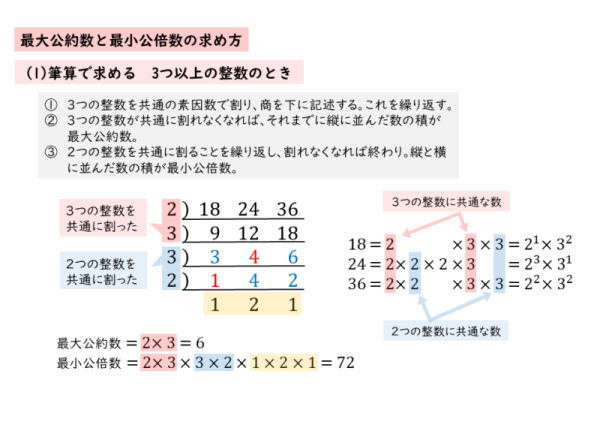
整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん

2

オリジナルの高校数学の問題を掲載していきます 問225 最大公約数の求め方

世界一分かりやすい算数 小５ 整数

2

最小公倍数とは 求め方や計算問題をわかりやすく解説 受験辞典

2

2

最大公約数問題

5年算数 整数の性質 公倍数 公約数の利用 長方形と正方形 マドリト フリーランスデザイナーのブログ

整数の最大公約数 最小公倍数の問題についてなのですが これはどういうこと Yahoo 知恵袋

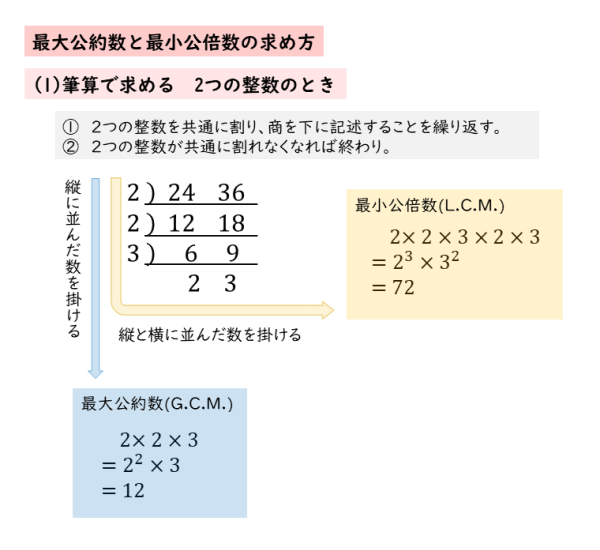
整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん

無料の学習プリント 小学5年生の計算ドリル 最大公約数 みそにゃch

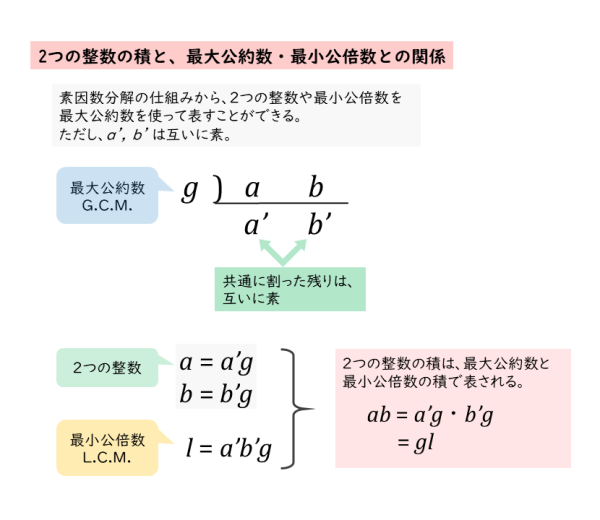
整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん

最大公約数レベル1 問題 385 400

公倍数公約数の筆算 レベル1 問題 160 180

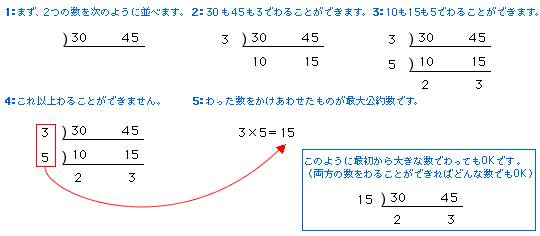
約数 公約数 最大公約数 算数の教え上手 学びの場 Com

２０１８年 東大理系数学 第２問の解説 数列 互いに素 最大公約数 理系と文系 オンライン受講 東大に 完全 特化 東大合格 敬天塾

通分に約分 最小公倍数に最大公約数 どんぐり問題５ｍｘ０３ 朝な夕な

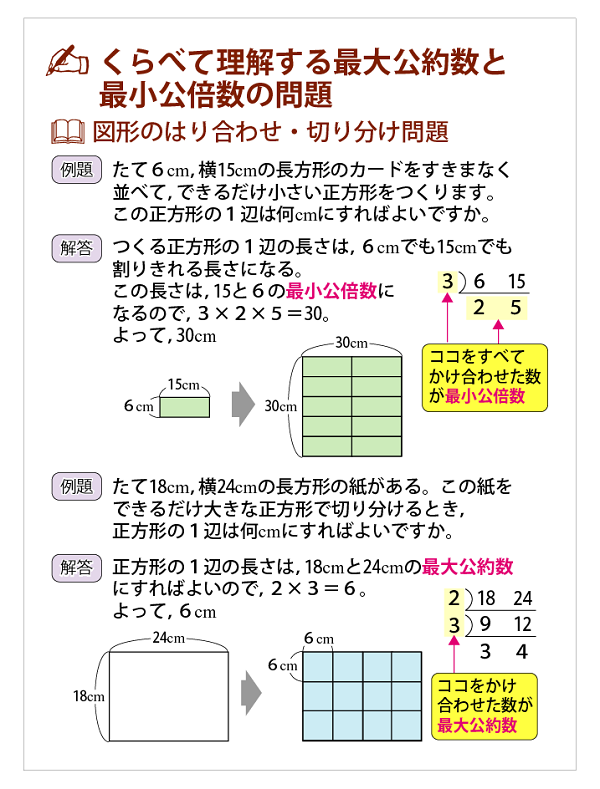
くらべて理解する最大公約数 最小公倍数の問題 恋する中高一貫校 適性検査 徹底攻略

マスラボ 小学校5年 算数 約数 レベル4 公約数の文章題 Youtube

ユークリッドの互除法による最大公約数の求め方 おいしい数学

最大公約数問題

５年算数整数 偶数奇数公倍数公約数 教え方

最大公約数の問題はこれで完璧 約数を漏れなく求める方法と公約数の見つけ方

約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材

小５ 算数 小５ 約数 公約数 最大公約数 Youtube

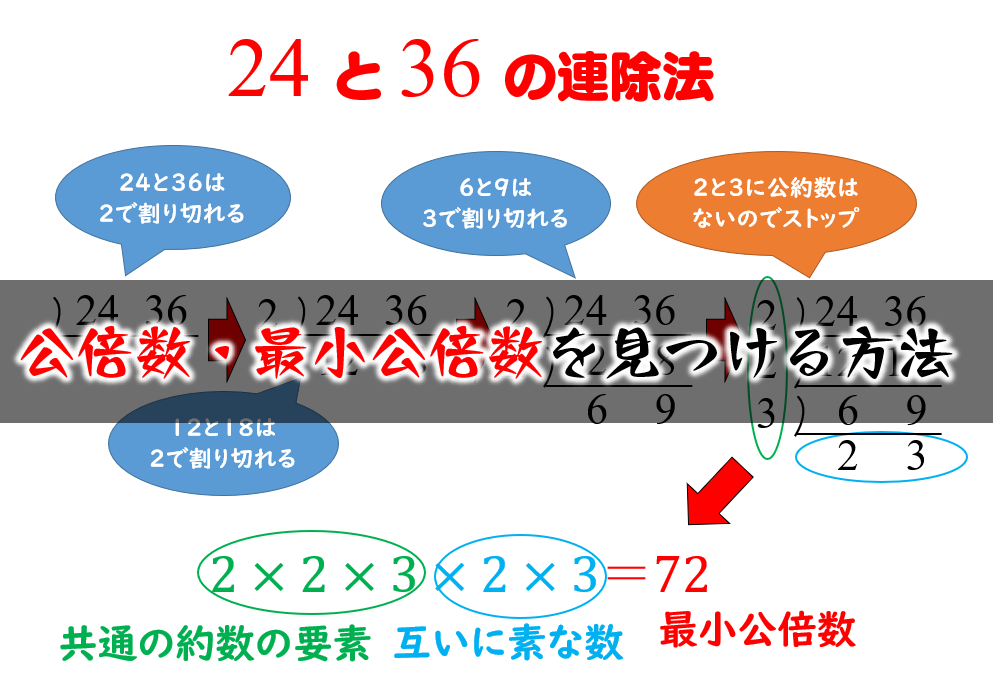
公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun

５年生の問題です 問題も最大公約数を出すんですか Yahoo 知恵袋

ユークリッドの互除法まとめ 証明 最大公約数 不定方程式 理系ラボ

最小公倍数 最大公約数 小学５年生 計算無料プリント 小学生算数問題

約数 公約数 最大公約数 約分 分数のたし算ひき算の授業 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材

整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん

ドリルズ 小学5年生 算数 の無料学習プリント 解説付き 倍数 約数の文章題

小学5年生の算数 動画 約数と公約数の問題 最大公約数 19ch

小学5年生の算数 動画 倍数 約数の文章題の問題 19ch

数学i Aチェック リピート 第6章 3整数の性質 2 最大公約数 最小公倍数 Pukiwiki

小学５年生 算数 8月 約数と公約数 公倍数 公約数の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ

最大公約数と最小公倍数の積の性質の２通りの証明 高校数学の美しい物語

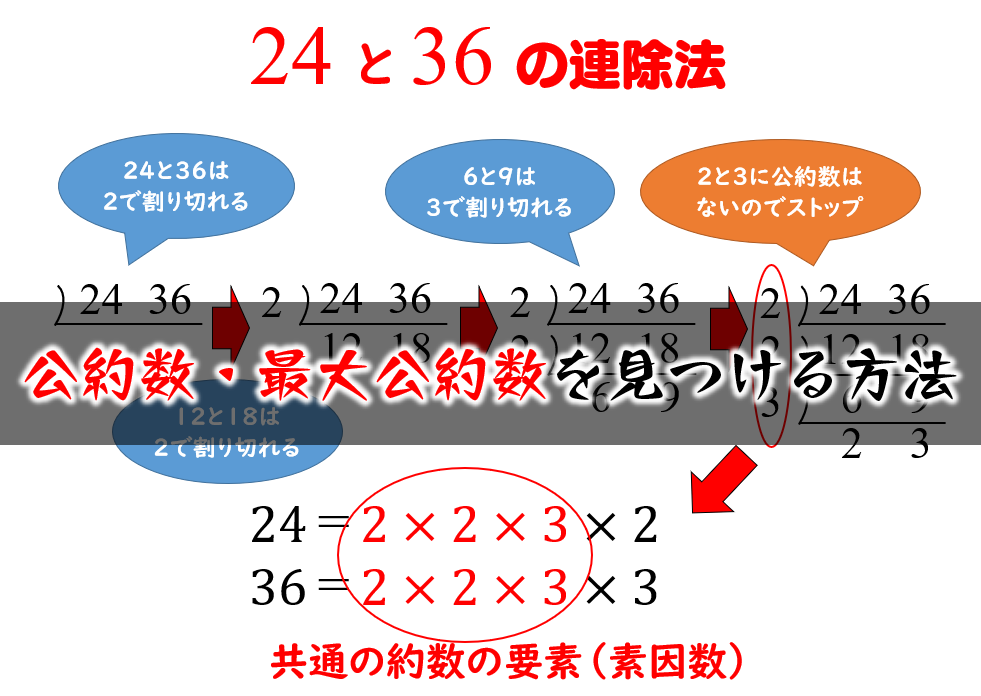
公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun

数学 For 大学受験 Twitter પર 問題 最大公約数が等しいことの証明 Mathworld4 整数の性質 最大公約数

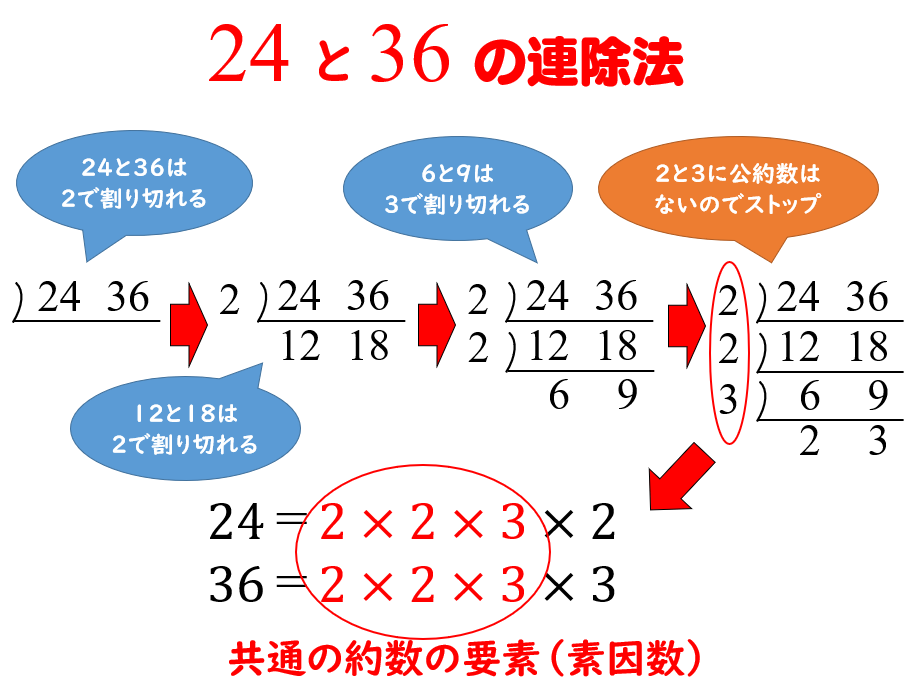
公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun

最大公約数を最速で求める方法 怜悧玲瓏 高校数学を天空から俯瞰する

公約数と公倍数の自主学習ノート例 家庭学習レシピ

１ の問題で これは最終的に最大公約数がｎとなるから一致するという 高校 教えて Goo

2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質

2

小学５年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生

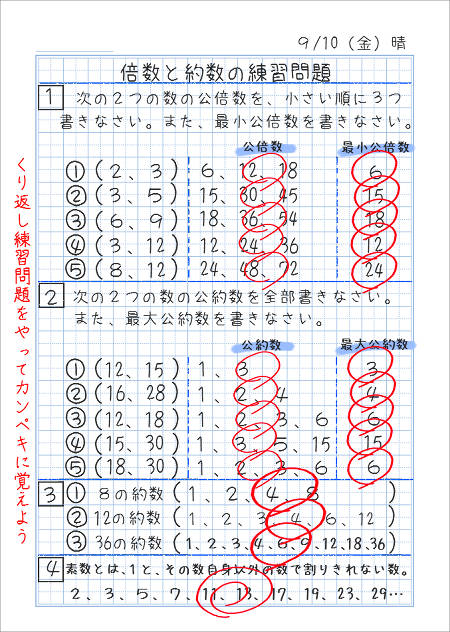
公約数と公倍数の自主学習ノート例 家庭学習レシピ

人気ダウンロード 公約 数 問題

中学受験 算数確認チェック15 数の性質 数の分解 グランパは元塾長

N 24 60の最大公約数が12 最小公倍数が1080のnをすべて求めよ Clearnote

2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質

この素因数分解を利用した問題についてなのですが Clearnote

最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ

3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ

高校数学a 最大公約数と最小公倍数の定義 受験の月

世界一分かりやすい算数 小５ 整数

最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場

Gcf 最大公約数 と Lcm 最小公倍数 の文章問題 ビデオ 数の性質 カーンアカデミー

高校数学 解説動画 数学a 整数の性質 最大公約数 文章題 数学

小５ 算数 小５ ２０ 倍数 約数の文章題 Youtube

最小公倍数 最大公約数のドリル

５年生 小学生向け手作り問題集 パパしゅく

問題 素因数分解と公約数の基本 中学 数学 理科の復習サイト

の問題が分かりません 簡単な方法や解き方を教えて下さい Clearnote

最小公倍数と最大公約数で タイル敷き詰め と 素数ゼミ 問題を解く 数学ia Himokuri

青チャートの整数の問題です Clearnote

2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質

中学受験の問題です 最小公倍数 最大公約数に関する添付の問題なの Yahoo 知恵袋

小学五年生の息子の宿題を 教えているのですが恥ずかしながら自信が Yahoo 知恵袋

最大公約数と最小公倍数の例題 京極一樹の数学塾

3

最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学

ドリルズ 小学5年生 算数 の無料学習プリント小学5年生 最大公約数と最少公倍数

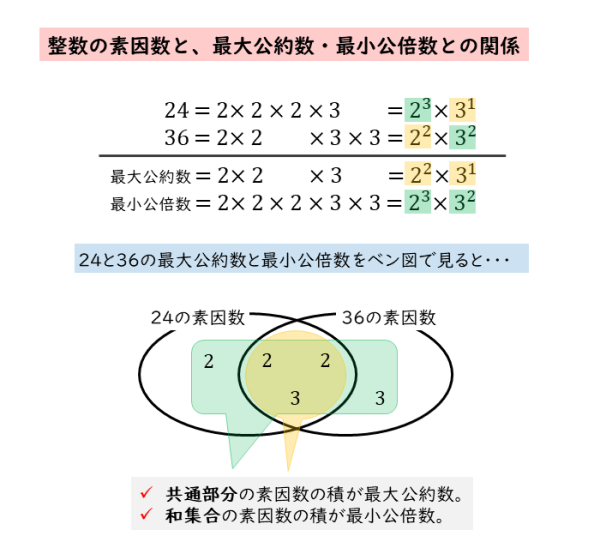
整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん

16 同志社大 最大公約数 最小公倍数 不定方程式 数学のコツ壺 風いま数学協室

3

５年生 小学生向け手作り問題集 パパしゅく

倍数と約数 最大公約数を求める 練習問題 Youtube