√100以上 おうぎ形の面積 ���校 209556-おうぎ形の面積 ���校

 円とおうぎ形の基本問題です。基本的な公式が分かっていれば簡単に出来るので計算ミスなどをしないよう確実に出来るようにしましょう。円とおうぎ形基本弦、弧、接線など19/2/9 2の問題文にミスがありましたので修正しました。 円とおうぎ形 計算練習中学1年生の平面図形、空間単元：複雑な面積の求め方 講師 下の図の影になっている部分の面積を求めてください。 生徒 扇形の半分の図形からうまく残りの白部分を引いた式ができれば解けそうですね。 講師 Goodです。 さてどのように引いたらよいでしょうか。 ヒントは、図おうぎ形は円の一部であることを理解させる。 3 おうぎ形の弧や面積は、同一円の中心角の大きさに比例していることを理解させる。 4 おうぎ形の弧や面積を自ら計算し、求めることができるようにさせる。 • 時間配当 1

簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

おうぎ形の面積 高校

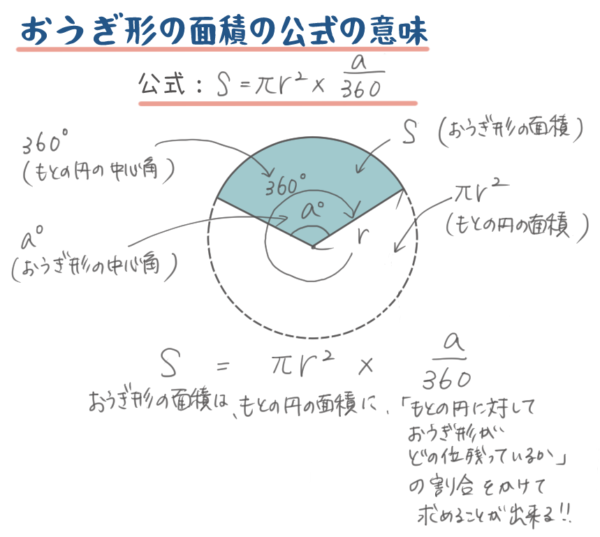
おうぎ形の面積 高校-(1) 面積を求めよ。 (2) 弧の長さを求めよ。 半径4cm で弧の長さが2πcmのおうぎ形がある。 (1) 半径4cmの円の円周の長さを求めよ。 (2) このおうぎ形は円の何分の一か。 (3) このおうぎ形の面積を求めよ。 (4) このおうぎ形の中心角を求めよ。 半径4cmで弧の長さがこの問題のポイント ・おうぎ形の孤の面積は、次の公式を使って求めることができます。 おうぎ形の半径をr、中心角をaとすると、面積Sは次の式で求めることができます。 S = π r 2 × a 360 おうぎ形の面積は、半径と中心角の大きさが判れば求めることができます。 もし、おうぎ形の孤の面積が、なぜこの公式で求めることができるのかについて、疑問に思った時

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

扇（おうぎ）形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形をエ 扇形の面積と弧の長さの求め方を考 えることができる。 ア 定規やコンパス，分度器などを使っ て，図形を平行移動したり，対称移動し たり，回転移動したりすることができ る。 イ 垂直二等分線，角の二等分線，垂線な どの基本的な作図ができる。おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 中心角40°の

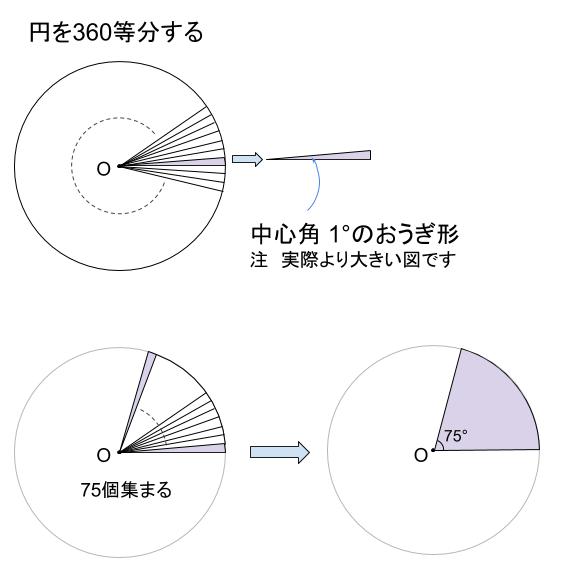
影の部分の面積、周の長さ（1）の解説 面積を求める場合には、大きな半円と小さな半円に分けて考えていきましょう。 それぞれの半径の大きさを間違えないように気を付けてくださいね！ 周の長さは3つのパーツ（赤、青、緑）に分けることができます。 それぞれを求めて、合計すれば周の長さとなりますね。 と はこれ以上は計算ができません。 扇形の面積の求め方の公式！ 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360 になるんだ。 つまり、 円周率×半径×半径×中心角÷360 ってわけさ。 たとえば、半径3cm、中心角が90度の扇形があったとしよう。 扇形の公式をつかってやれば、 S = 3×3×π×90/360 = 9π/4 になるんだ。 どんなこの中心角 \(1°\)のおうぎ形が \(75\) 個集まると、その面積は 円の面積\(×\displaystyle \frac{1}{360}×75\) これがおうぎ形の公式の意味するところです。 おうぎ形の面積 もう1つの方法 おうぎ形の面積には、もう \(1\) つ覚えておいて損のない公式があります。

平面図形 おうぎ形の中心角の求め方 おうぎ形の中心角を求める問題で，わかっている数字が変わると求め方がわからなくなります。 進研ゼミからの回答 ここで紹介している内容は17年3月時点の情報です。ご紹介している内容 円とおうぎ形の作図の仕方や面積の求め方など そして回転体の表おうぎ形の問題では弧の長さや面積を求める問題が出題されますが、それぞれ以下の公式で求めることができます。 おうぎ形の面積 ＝ 円の面積 × 中心角 360° 中 心 角 360 ° ＝ 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と おうぎ形は円の一部と考えるのが基本的でしょう。 上の図で、円の面積は π r 2 となります。 これを中心角 x 分だけ切り取ればいいので S = π r 2 × x 360 となります。 基本的にはこれで十分です。 次に、おうぎ形の弧の長さ l についても考えてみ

中学数学 基礎的な図形問題の解法2選 21年度 東海高校 勉強 Youtube スタディチューブ

簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

 扇形の弧の長さと面積 公式 扇形の弧の長さと面積 半径r、中心角θ、弧の長さl、面積Sとすると \(・l＝rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\) 証明 比率による証明 証明 \((円周)=2πr\)より \(θl=2π2πr\) ⇒ \(l=\frac{2πrθ}{2π}\) \(=rθ\) よって \(l＝rθ\) また \((円の面積)=πr^2\)より長方形・正方形の面積（基本）の面積を求める基本問題です。 面積のもとめ方の基本をしっかり確認しましょう。 面積とは 広さのことを面積といい、1辺の長さが1cmの正方形の面積を1㎠（1平方センチメートル）といいます。 長方 」）を 求める問題を解くコツについて まとめます。 中1おうぎ形の面積は 半径×半径×円周率×中心角÷360 でした。 いま半径は2 cm・中心角は45°・円周率は314だと分かったので，式を組み立てると， 面積=2 ×2 ×314×45÷360 となります。 あとはこの式を解いていくだけです。 × の値は前述より8であるため， 面積＝ (2× )× (2× )×314×45÷360=4× × ×314×45÷360=4×8×314×45÷360=314=1256 (cm2) と値を求められました。 以上をまとめる

円とおうぎ形 応用 無料で使える中学学習プリント

扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題

円錐の表面積の求め方 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年～中学3年生内容計算の基礎養成演習時間割50分授業×週1回授業回数月間4回授業料中学1年生：8,300円中学2年 おうぎ形の面積の求め方 中学生 数学のノート Clearnote 表紙 1 2 3 公開日時 21年12月29日 17時19分 更新日時 22年03月29日 00時06分 中学生 アの面積は 10×10÷2＝50（㎠） イの面積は 10×10×314÷4ー50 ＝285 （㎠） イ÷ア 50÷285 ＝057 よって ア：イ＝1：057 上の考え方を使うと下の正方形と色のついた部分の面積比も 1：057 になる。 正方形の面積＝,10×10＝100 （㎠） 100：面積＝1：057 面積＝57㎠ と求めることができる。 円周率が314の時しか使えません。 公式として覚えているだけでは、中学生

公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ

おうぎ形の弧の長さと面積 が苦手でもコレなら分かる 中学1年数学 平面図系 教科書をわかりやすく通訳するサイト

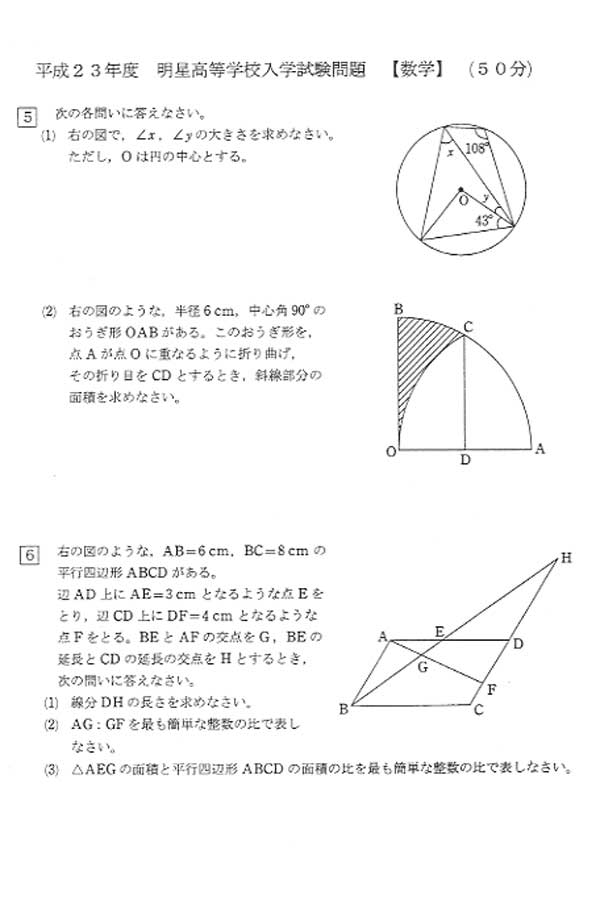
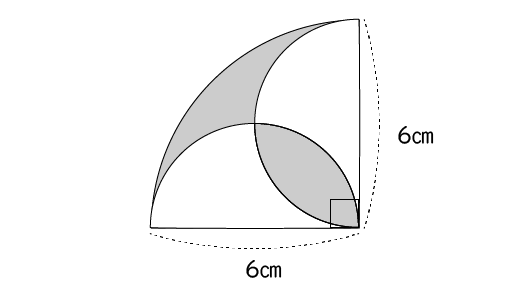
 おうぎ形の半径は、正方形の一辺の長さと等しく、 6cm 6 c m です。 また、中心角は、正方形の1つの角と等しいので、 90∘ 90 ∘ です。 以上から、面積は 62 −62 ×π × 90 360 = 36 −9π 6 2 − 6 2 × π × 90 360 = 36 − 9 π なので、 (36−9π)cm2 ( 36 − 9 π) c m 2 となり半径16cmで中心角315°のおうぎ形の弧の長さを求めよ。 半径12cmで中心角80°のおうぎ形の面積を求めよ。 半径10cmで中心角°のおうぎ形の面積を求めよ。 半径 9 2 cmで中心角160°のおうぎ形の面積を求めよ。 半径3㎝、中心角1°のおうぎ形がある。 弧の長さを求めよ。 中1第51回円とおうぎ形①（弧の長さと面積）の解答解説はこちらから印刷できます。 → 中1第51回円とおうぎ形の計量①（弧の長さと面積）（解答解説） 中1第51回円とおうぎ形①（弧の長さと面積）の授業映像は下をクリックしてご覧ください。 中1「1から学ぶ高校受験数学シリーズ」 author

おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方

弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか

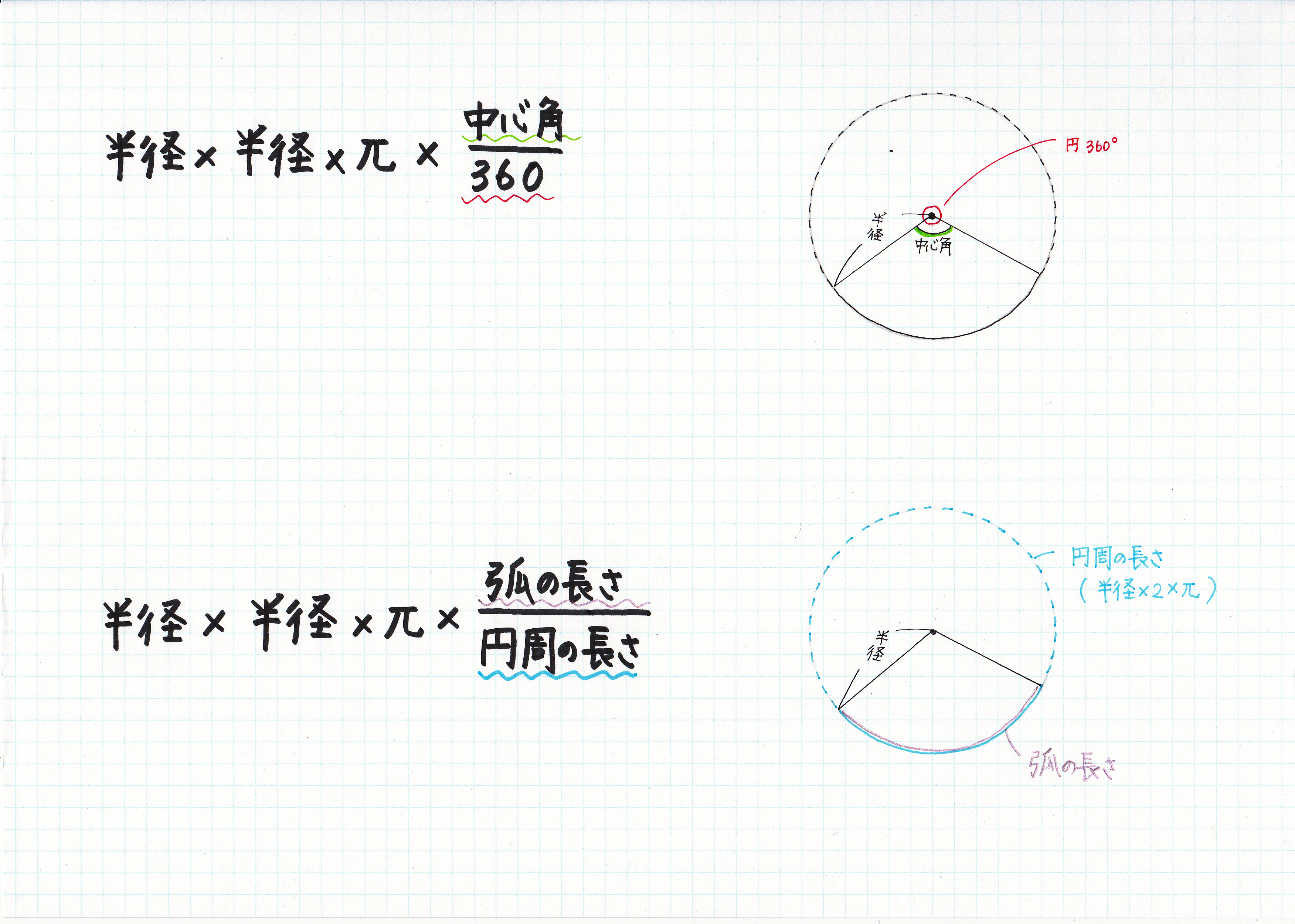
まずは、円の面積と円周の求め方をおさらいしましょう。 円の面積 半径 × 半径 × 円周率 ( 314) ですが、中学では、半径 = r , 円周率 = π として、次のように表します。 r × r × π = π r 2 円周 直径 × 円周率 ( 314) ですが、中学では、半径 = r , 円周率 = π として、次のように表します。 2 × r × π = 2 π r ※ π をかく順番は数字の後、文字の前になります。 よっておうぎ形の面積は 答． ㎠ と出ます。 弧の長さから割合を出す 例題3）半径 cm、弧の長さ cmのおうぎ形の中心角を求めよ。 この例題3は、中心角・弧・面積のうち「弧の長さ cm」がわかってます。 そんで半径 cmの円全体の円周は (cm)です。 よって割合は おうぎ形 円全体 また、求めるものは「中心角」なので、まず円全体の中心まわりは ° よっておうぎ形の中心角は高校入試に挑戦1、どうだったかな？ 続いて2，3もやってみよう！ ・小6算数（円とおうぎ形の面積／立体図形）高校入試に挑戦2 https//youtube/Tl

日本の学校 大学 短期大学 専門学校の進学情報なら日本の学校

2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく

 よく出るおうぎ形に関する対策問題の解答 ①12π （公式）おうぎ形の面積=円の面積×中心角/360 ②12π （公式）1/2×半径×弧の長さ ③60π （公式）母線×半径×π ④1° （公式）（おうぎ形の面積/円の面積）×360 頂点から垂線を下ろして三平方の定理を利用する。 高さをhとすると h 2 =8 2 2 2 =644=60 h＝2√15 求める体積は 1/3×2×2×π×2√15 ＝8/3√15π（3分の8ルｰト15） （2）円錐を展開してできるおうぎ形の中心角なので、中心角をxとして、「母線×中心角＝半径×360」を利用すると 8×x＝2×360より、x＝90°となる。 （3）側面んの展開図のおうぎ形＝円錐の側面積なのでおうぎ形って円の一部だから、おうぎ形の面積＝円の面積の一部です。 だから(円の面積)× \\(\\frac{1}{4}\\) をすればいい。 円の面積は円の面積の求め方をいろいろ考える。 円を半径で16等分，32等分したおうぎ形を，求積公式を知っている形 に並べ替える。 長方形に並べ

高校入試と 円とおうぎ形 中学生 受験対応 英語 数学 学習講座

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

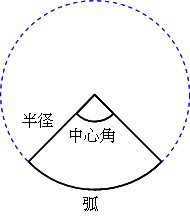
 おうぎ形の面積 半径 、中心角 のおうぎ形の面積 は で求めることができる。 先程の弧の長さと同様に円の面積と異なるのは がついている ということです。 これもおうぎ形が 円の面積のどのくらいを占めているのか を表しています。 例えば中心角が正方形の面積が4a 2 円の面積が π a 2 だから 扇形の高校入試問題（面積） 問題11 右の図のように，半径3cm，中心角1°のおうぎ形OABがあります。 このおうぎ形の面積を求めなさい。 ただし，円周率は を用いなさい。 （北海道15年） 解説を見る 円全体の面積は (cm 2 )だから 中心角が1°のおうぎ形の面積は (cm2)（答） →閉じる← 問題12 右の図のような，半径2cm，中心

中学数学 Dcの長さを求めよ 灘高 勉強 Youtube スタディチューブ

扇形の面積の求め方 公式と計算例

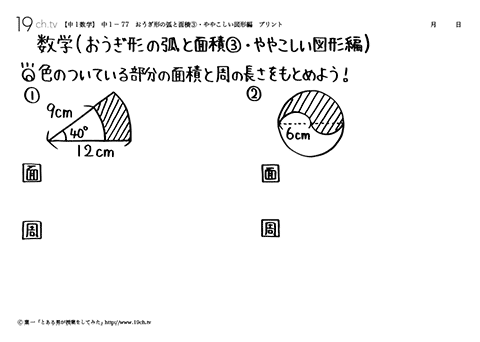
中学１年の数学 動画 おうぎ形の弧と面積 ややこしい図形編の問題 19ch

扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち

日本の学校 大学 短期大学 専門学校の進学情報なら日本の学校

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

おうぎ形 注意 周りの長さを求める公式を解説 数スタ

円とおうぎ形 応用 無料で使える中学学習プリント

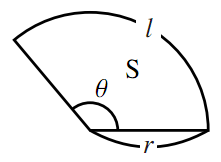
扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext

高校入試数学 おうぎ形についての公式まとめとその練習問題 トルテン

標準 おうぎ形と正方形の面積 なかけんの数学ノート

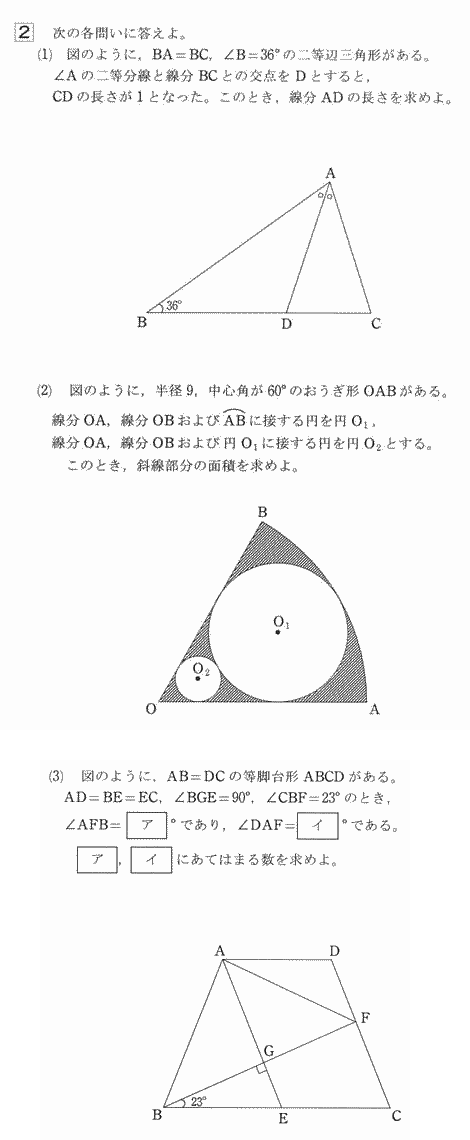
城北高校17年度数学入試問題 2 平面図形 医学部受験ならプロ家庭教師集団スペースone 公式 中学受験からオンラインも対応

扇形の中心角の求め方を教えてください 中心角の求め方は２通りのパタ Yahoo 知恵袋

3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ

3

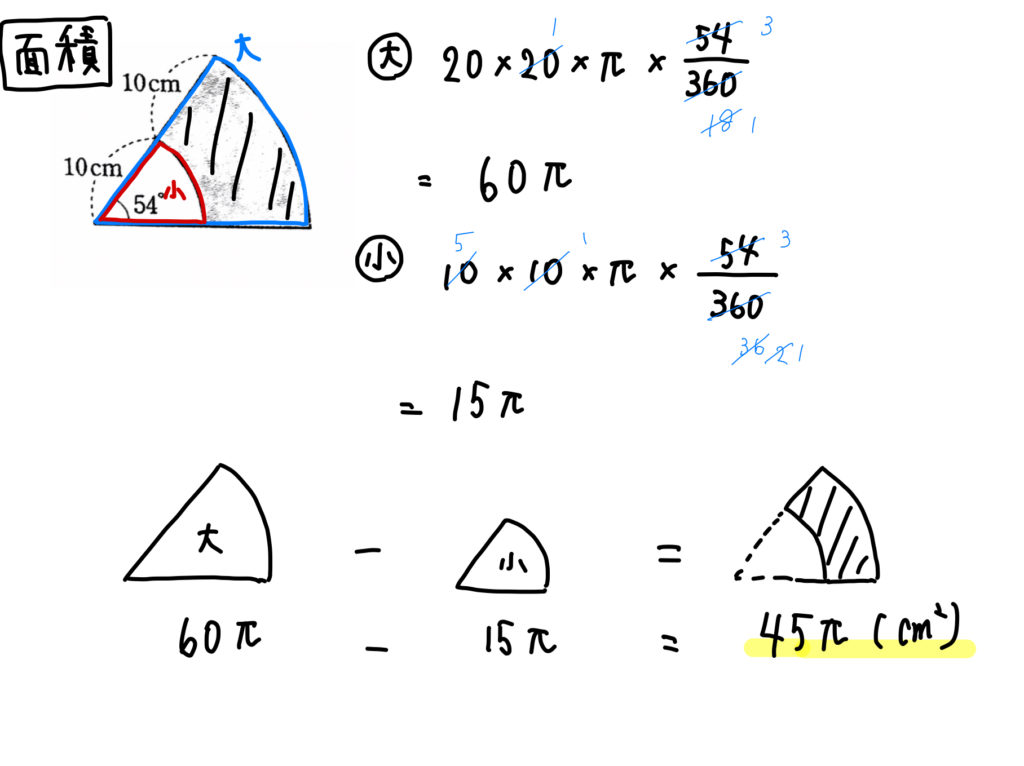
おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ

扇 おうぎ 形の面積を求める公式と弧の長さの求め方

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

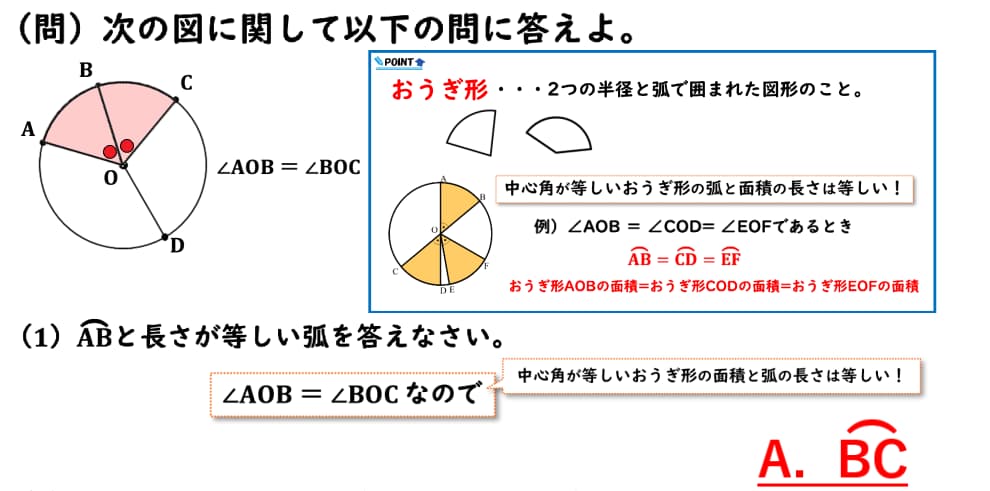
空間図形 おうぎ形について動画で丁寧に解説 中1数学 家庭教師のlaf

高校入試数学 おうぎ形の弧の長さと面積 小問対策 Youtube

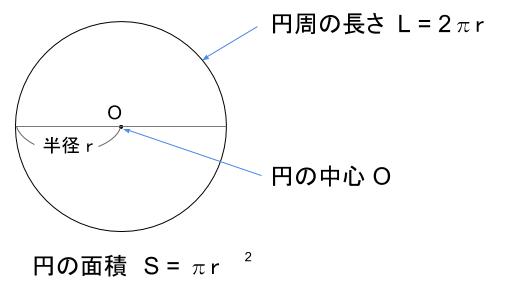
中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su

中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su

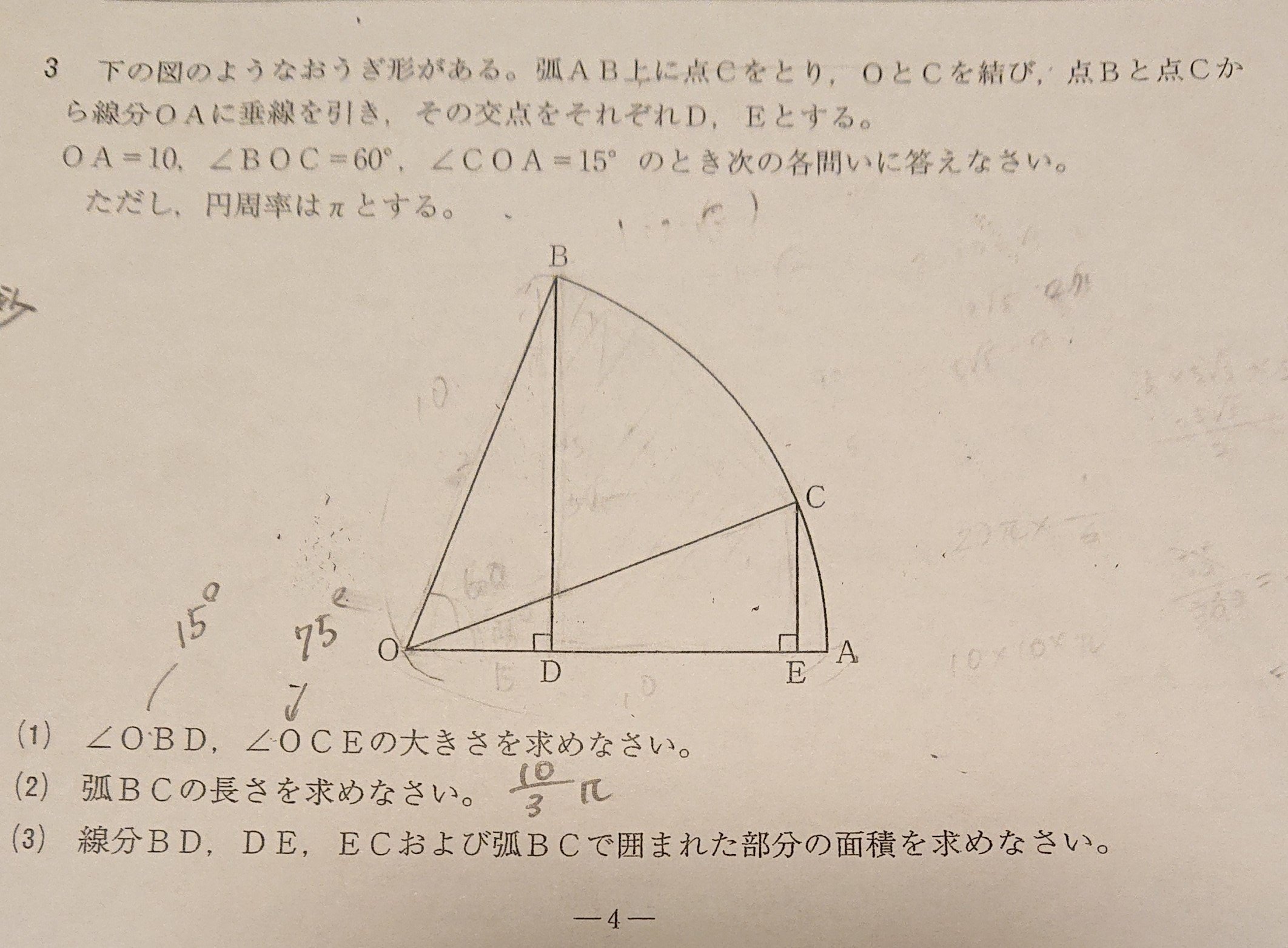
おうぎ形の面積 Twitter Search Twitter

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube

山と数学 そして英語 小学校算数 おうぎ形を含む図形の面積の難問

高校受験対策 図形１０ 面積 の問題 動画 19ch

夏休み 超お得な無料プレゼント企画 無料 学習 夏休み

円錐の表面積の求め方

Proceedx 学習ポスター0978中学数学重要公式集 高校入試対策 送料無料 勉強部屋 教室 壁掛け 中学

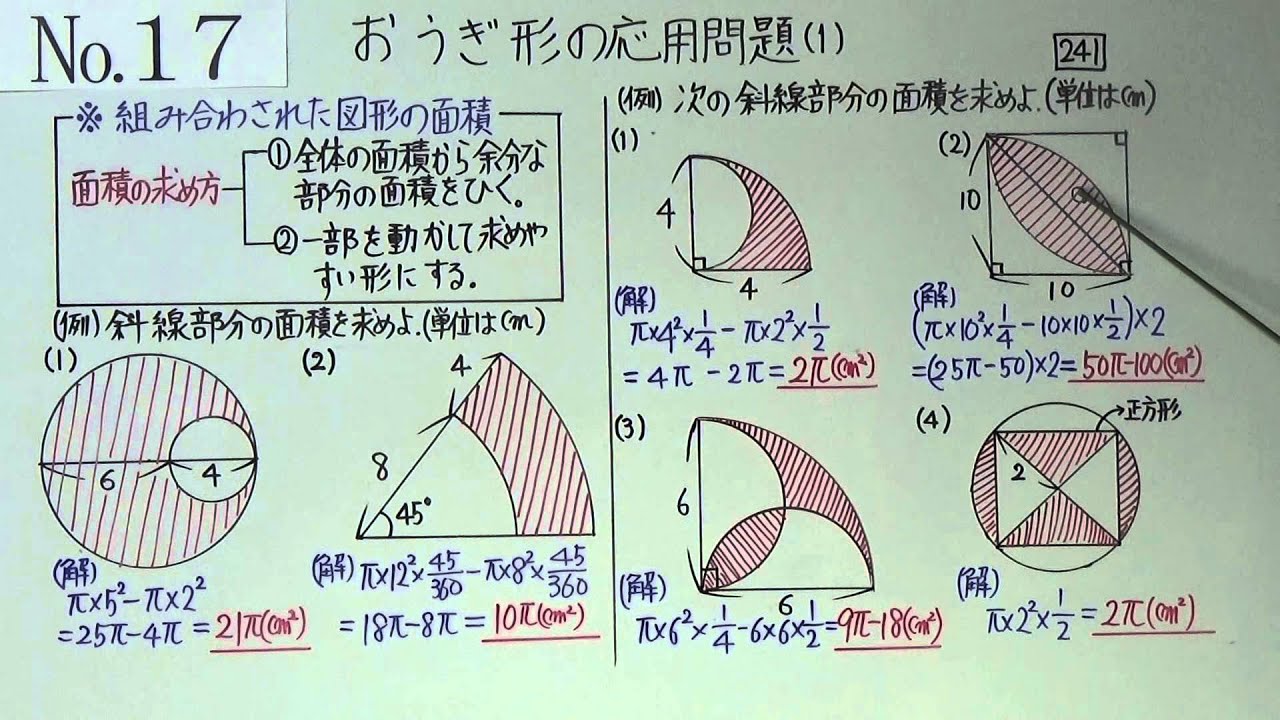
中１ １７ ２ おうぎ形の応用 １ Youtube

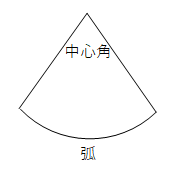
中1数学 おうぎ形の公式 Examee

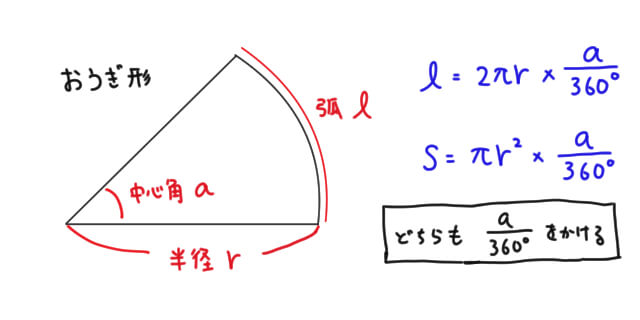
おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

数学パズル 意外と悩むおうぎ形の面積問題 ひらめいたらスッキリします 暇つぶしに動画で脳トレ

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

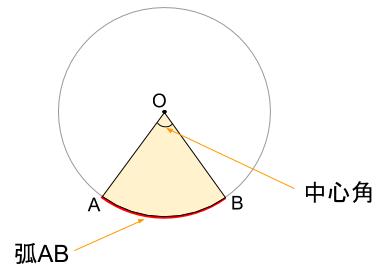
中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

三角形の面積を求める公式７選 高校数学のまとめにどうぞ

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

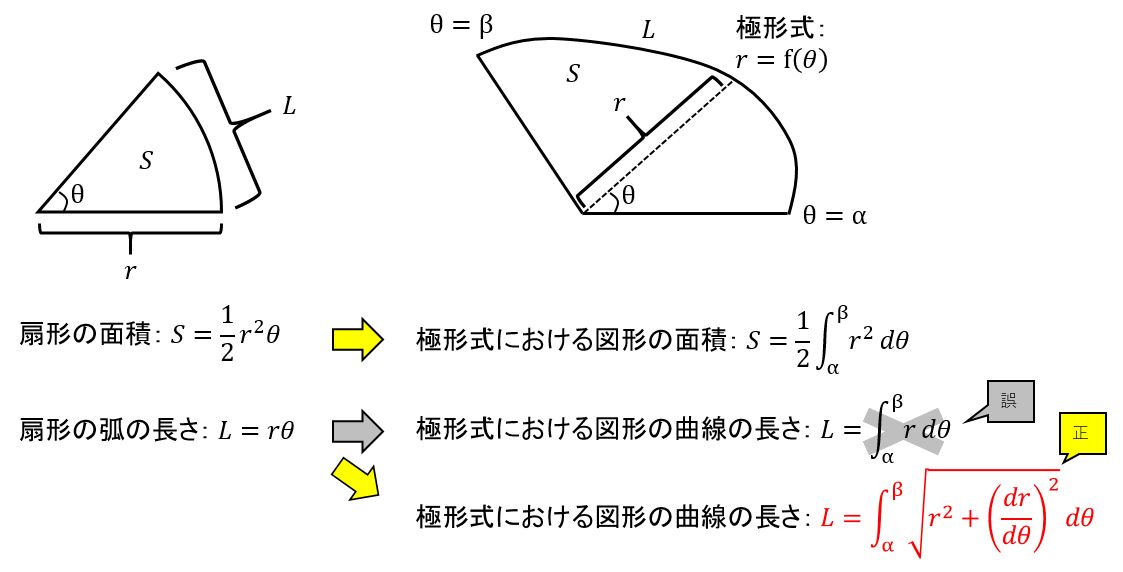
Lさんはtwitterを使っています 今ミスしたことをまとめました 極形式について 面積は扇形から公式が作れるのですが 曲線の長さは扇形から作れません D 作れない理由は Rとr 2における近似レベルの違いな気がしますが 詳細は調べてません 数学

1

三角形の面積を求める公式７選 高校数学のまとめにどうぞ

平面図形 おうぎ形の中心角 中学数学 定期テスト対策サイト

3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ

おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ

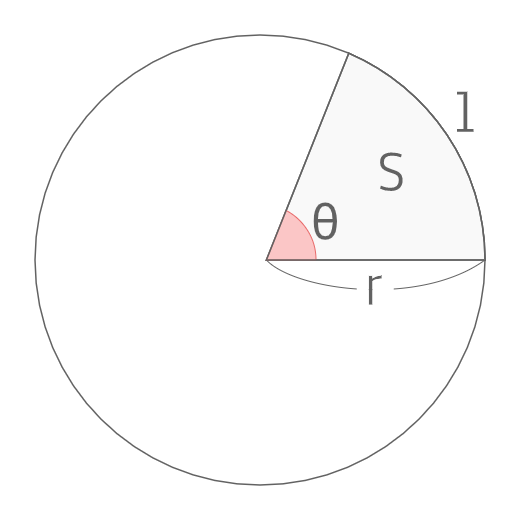
高校数学 扇形の弧の長さと面積 の公式とその証明 Enggy

すらら X 坂城高等学校 地方の公立スタンダード高校における主要3科目での個別最適化学習の実現 未来の教室 Learning Innovation

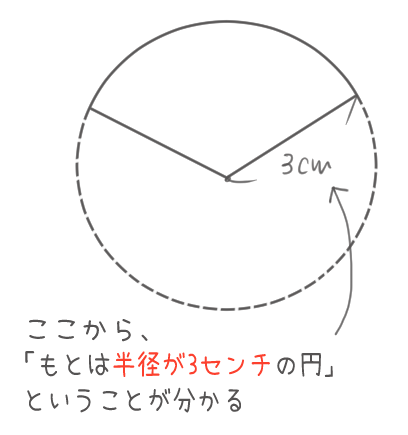
おうぎ形の弧の長さと面積 が苦手でもコレなら分かる 中学1年数学 平面図系 教科書をわかりやすく通訳するサイト

三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか

扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー

おうぎ形 Twitter Search Twitter

円 扇形 の面積 周や弧の長さの公式 数学fun

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw

数楽楽 愛知県高校入試 数学 の解説サイト

おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ

1

高校入試数学 おうぎ形についての公式まとめとその練習問題 トルテン

カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw

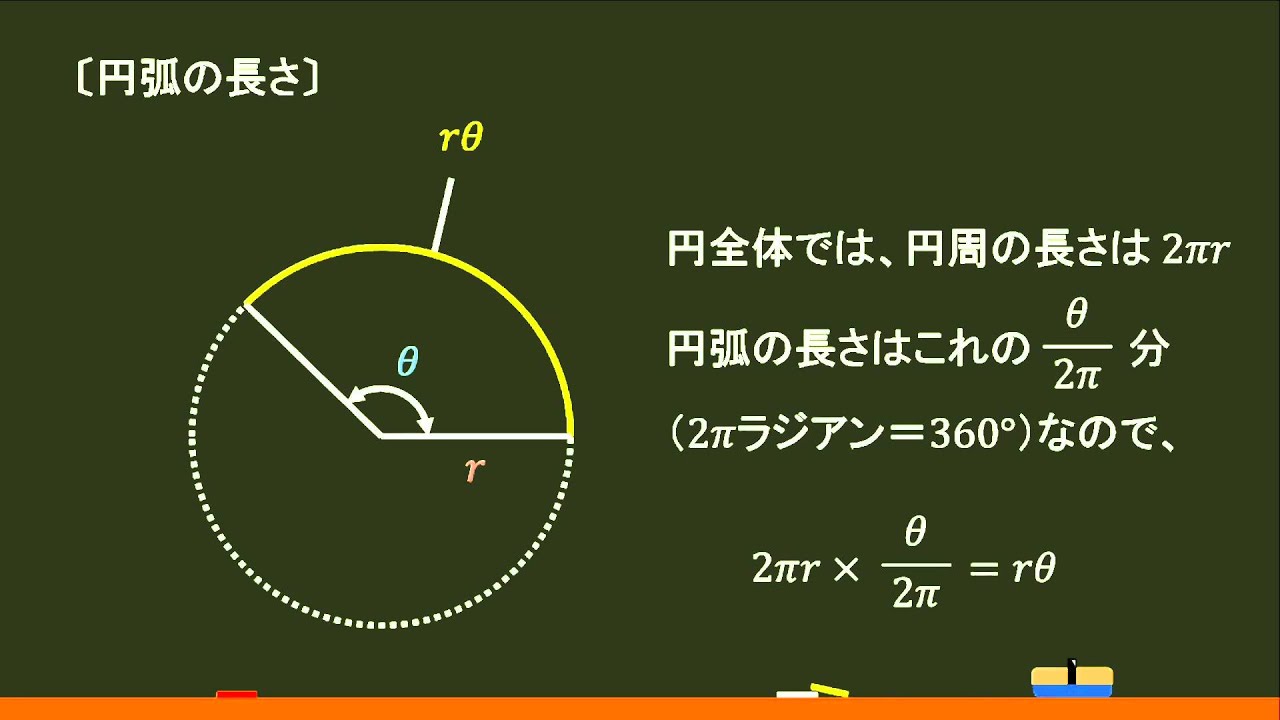
数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube

高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月

高校入試対策数学 円錐に関する対策問題 Pikuu

高校入試対策数学 平面図形問題 円 おうぎ形の面積 弧の長さ 斜線部分の面積 相似 特別な直角三角形の問題 Youtube

平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト

高校入試数学 おうぎ形についての公式まとめとその練習問題 トルテン

円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張

円 扇形 の面積 周や弧の長さの公式 数学fun

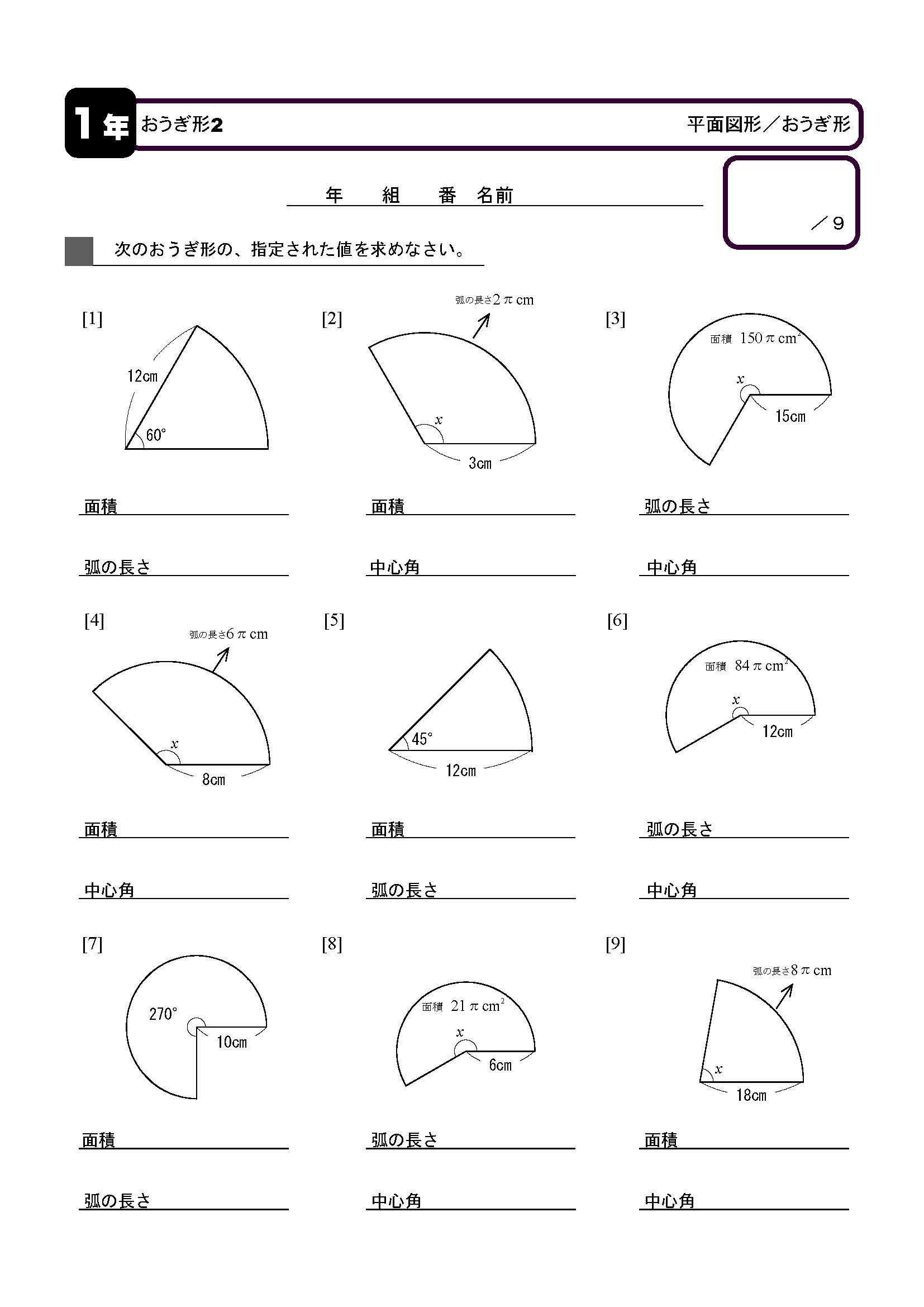
モノマナビ研究所

おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

おうぎ形について 小6 中1 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

なぜ おうぎ形の面積は１ ２ 弧の長さ 半径 なのか を説明します おかわりドリル

ヤフオク 算数 難関私立中学受験 高校受験対策に 革命的

扇 おうぎ 形の面積を求める公式と弧の長さの求め方

中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su

扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典

円とおうぎ形 無料で使える中学学習プリント

弧の長さは分かったんですけど 面積の求め方がよく分からないんですlll Clearnote

Mathematics 平面図形 おうぎ形 働きアリ

高校入試の直前対策として おうぎ形のまとめ ワード数学ラボラトリ Microsoft Word And Math Facebook

中心角 Klcブログ

高校入試の直前対策として おうぎ形のまとめ ワード数学ラボラトリ Microsoft Word And Math Facebook

公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ

中学校1年生数学 複雑な面積の求め方 成果主義 Itto個別指導学院 長野市の学習塾

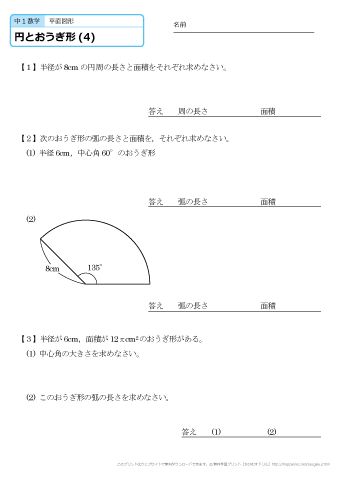
中学１年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中1数学 おうぎ形の公式 例題編 映像授業のtry It トライイット

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

Incoming Term: おうぎ形の面積 高校,